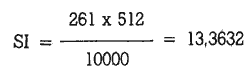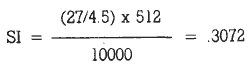La tecnica di "table look-up" è diventata il metodo più comune per generare segnali audio periodici con mezzi digitali. Essa permette un compromesso tra i requisiti di un suono di alta qualità e il desiderio di ottenere dei risultati con la maggiore efficienza possibile. Uno dei grossi vantaggi del "table look-up" sta nella composizione della tabella stessa.

Si possono infatti generare tabelle che rappresentano qualsiasi combinazione di parziali in qualsiasi proporzione di ampiezza si desideri; naturalmente, ciò conduce a sperimentare combinazioni di parziali che non esistono, o magari non possono affatto esistere, negli strumenti acustici tradizionali; oppure combinazioni che possono essere difficili da realizzare con sintetizzatori analogici, ed impossibili da controllare in modi musicalmente interessanti con questo tipo di strumenti, a meno che non si tratti di apparecchi dotati di sistemi digitali di controllo.

Rivediamo brevemente come lavora il "table look-up". Vogliamo produrre un'onda di suono che è di natura periodica, cioè ripetitiva o ciclica. Innanzitutto ci occorre che il calcolatore generi una serie di numeri per rappresentare un ciclo di quest'onda; poi bisogna far ripetere continuamente al calcolatore questa serie ad una determinata velocità (cicli al secondo, o frequenza) in modo da far convertire dal nostro convertitore DAC (da digitale ad analogico) questi cicli di numeri in un segnale audio di quella particolare frequenza. Se questa serie di numeri è costituita dai valori derivati da una funzione circolare di seno oppure di coseno, otterremo un tono sinusoidale dal calcolatore. Ora, secondo una teoria molto usata, ogni funzione periodica complessa può essere scomposta in una somma di funzioni di seno e coseno. Per il musicista ciò significa che dovremmo essere capaci di costruire qualsiasi suono esistente o anche finora non esistente, addizionando tra loro gli appropriati toni sinusoidali alle appropriate frequenze ed ampiezze.

Così, per un tono che si approssima ad un'onda di rampa noi potremmo chiamare simultaneamente 10 toni sinusoidali, con frequenze 1, 2, 3, 4, ... 9, 10 volte la frequenza fondamentale, e ampiezze 1/1, 1/4, 1/9, 1/16, ... 1/81, 1/100 dell'ampiezza della frequenza più bassa. Se dobbiamo calcolare il valore di seno per ogni armonica in quest'onda ad ogni campione, abbiamo in mano una procedura computazionale enormemente lunga.

Ma tenete presente che abbiamo a che fare con cicli di numeri; così, invece di ripetere inutilmente gli stessi calcoli per ogni ciclo, noi calcoliamo il valore di seno per un ciclo di un'onda di seno prototipo che contiene già la somma delle 10 armoniche alle ampiezze volute; immagazziniamo questi valori nella memoria del calcolatore sotto forma di una tabella indirizzabile (ciascun valore è immagazzinato in una locazione unica nella memoria del calcolatore e ci si può riferire ad esso mediante l'indirizzo associato con quella locazione); poi semplicemente programmiamo il calcolatore ad emettere i valori della tabella alla frequenza che desideriamo. Questa frequenza determina le successioni di indirizzi a cui il calcolatore deve andare per ottenere la serie di valori dalla tabella dell'onda di seno.

Ciascun punto particolare nella tabella di seno è chiamato fase, poiché questi valori sono derivati da cicli che si riferiscono alla funzione circolare di seno. Il fattore che dice al calcolatore quale fase dell'onda di seno consultare per ciascun suono è chiamato sampling increment ("incremento di campionamento", abbreviato SI) ed è in relazione con la frequenza del segnale in base alla seguente equazione:



dove F = frequenza, TL = misura o numero di punti nella tabella, e SR = "sampling rate", ossia numero di campioni da calcolare per un secondo di suono.

Il corretto indirizzo di tabella o fase (PHS) viene calcolato per ogni campione aggiungendo ripetutamente il sampling increment alla fase, secondo l'equazione:
PHS = PHS + SI

Questa equazione viene eseguita una volta per ciascun campione. Quando PHS diviene maggiore di
TL allora esso viene aggiustato facendo:
PHS = PHS - TL

Se la nostra frequenza è un do centrale (261 Hz), il corretto sampling increment per una tabella con 512 full word, a 10.000 campioni al secondo è:




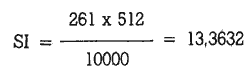
Poiché la tabella ha solo numeri interi per indirizzi, ne risulta una certa imprecisione; per ogni campione successivo, il calcolatore guarderà alla seguente serie di locazioni: 0, 13, 26, 40, 53, 66, 80, 83, 106, 120 ... e andrà a prendere valori a queste locazioni (i valori di seno desiderati), da mandare, alla fine, al convertitore. Quanto maggiore è la dimensione della tabella, tanto minore sarà la precisione della serie di fasi; ed anche, quanto maggiore è la misura della tabella, tanto più memoria ci vuole, e questo può divenire un problema costoso.

La dimensione della tabella con 512 locazioni è un buon compromesso tra i requisiti di un segnale audio pulito ed il mantenimento entro limiti ragionevoli della memoria richiesta. Potete aumentare significativamente la precisione ed anche ridurre la richiesta di memoria aggiungendo una procedura di interpolazione che tiene conto della parte frazionaria di ogni sampling increment: ma, come sempre, quel che si risparmia da una parte si spende dall'altra: il table lock-up con interpolazione è almeno del 50% più lento del processo normale, il che significa che il tempo di calcolo viene aumentato notevolmente.

Usi della procedura di table look-up

Chiaramente, l'uso fondamentale del table look-up consiste nel generare un segnale audio; si crea una tabella di onda di seno scrivendo un programma che chiamiamo in azione ad un certo momento durante l'esecuzione, e si dà a questa tabella un indirizzo di riferimento (ad esempio il numero 3) che dice al programma di table look-up di guardare la nostra terza tabella ogni volta che occorre generare un'onda di seno.

Si devono osservare le convenzioni nel linguaggio di programmazione che si sta usando, che consentono al programma di table look-up di trovare la tabella di seno precedentemente generata In molti linguaggi, si dichiara semplicemente all'inizio di entrambi i programmi che una particolare area della memoria sarà designata dallo stesso nome in ciascuno di essi: chiamiamola semplicemente F (come Funzione) e, come in Fortran, scriveremo qualcosa come:

(table look-up) (funzione generatrice della tabella di seno)
Subroutine Tab Subroutine Sine Common F (512) Common F (512) etc... etc... dove la parola COMMON
(comune) dice al calcolatore che l'area di memoria F, con 512 locazioni, è la stessa per entrambi i programmi (o "subroutines"). Per motivi di convenienza, il processo di table look-up come generatore di segnale è stata tradizionalmente chiamata subroutine di oscillatore, poiché dà un risultato audio che è
identico ad un oscillatore analogico ideale; ma che oscillatore!

E' infinitamente più facile da controllare, ha una precisione totale, non può dare distorsione, a meno che non gli facciate produrre numeri più grandi della capacità del vostro calcolatore, e per mezzo di procedure computazionali complesse può fare cose che sarebbero impensabili con un oscillatore analogico qualsiasi.

Proprio come un oscillatore di un sintetizzatore analogico standard può controllare vari parametri di altri oscillatori, o filtri o inviluppi (mi riferisco al concetto analogico di controllo di voltaggio), così l'oscillatore digitale può fare esattamente le stesse cose, ma meglio e con molto maggior precisione. Tuttavia, bisogna dare al programma di oscillatore valori dei dati che siano l'equivalente dei voltaggi di controllo nel sistema analogico; e bisogna essere in grado di disegnare una tabella di valori che corrisponda proporzionalmente all'aumento o alla diminuzione nel tempo dei valori di controllo prescelti. Per esempio, se vogliamo generare un glissando, dobbiamo riuscire a far sì che la frequenza (input alla nostra subroutine di oscillatore che genera il tono di seno) si elevi o scenda in un periodo di tempo richiesto.

Con la otteniamo solo un glissando che cresce; con lb solo uno che cala; con 1c una crescita seguita da diminuzione. Il grafico 1 c rappresenta la situazione più conveniente, perché possiamo ottenere anche il glissando crescente leggendo solo la prima metà della funzione e quello diminuente leggendo solo la seconda metà. Se questa tabella viene letta da una subroutine di oscillatore, possiamo aggiustare il SI a seconda di quanto veloce vogliamo che sia il glissando. Supponiamo di volere un intero ciclo di glissando su e giù (grafico 1 c) in un tempo di 3 secondi; 1 ciclo in 3 secondi significa .3333 cicli per secondo. Il Sampling Increment è calcolato come:

Un altro tipico uso della subroutine di oscillatore è quello di generare inviluppi di ampiezza, esattamente nello stesso modo in cui un generatore di inviluppo analogico modella le caratteristiche di ampiezza nel tempo di un suono. Qui l'oscillatore è usato per modellare il livello audio istantaneo; i valori nella tabella che voi create sono proporzionali al livello di voltaggio, cioè l'ampiezza del segnale a qualsiasi momento dato. Il punto è che siamo liberi di disegnare qualsiasi forma di inviluppo vogliamo e poi di manipolarla in qualsiasi maniera ci piaccia.

Naturalmente queste qualità dipendono dalla velocità con cui l'oscillatore di inviluppo legge queste tabelle come controlli di ampiezza, il che, ancora una volta, si ottiene calcolando il SI.

Se, ad esempio, vogliamo 27 attacchi (cicli, in questo caso) in 4 secondi e mezzo, scriviamo:

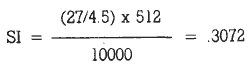lasciando al calcolatore il problema di calcolare quanti cicli al secondo sono necessari per ottenere 27 attacchi in 4.5 secondi. Otterremo una serie piuttosto veloce di attacchi che renderà 2a e 2c simili tra loro, mentre 2b comincerà a sembrare come della musica suonata a rovescio con un registratore.